ANÁLISIS VECTORIAL II

ANÁLISIS VECTORIAL II

SUMA VECTORIAL

Sumar 2 o más vectores, es representarlos por uno sólo llamado RESULTANTE. Este vector resultante produce el mismo efecto que todos juntos.

Hay que tener en cuenta que la suma vectorial no es lo mismo que la suma aritmética.

|R|=A+B+C

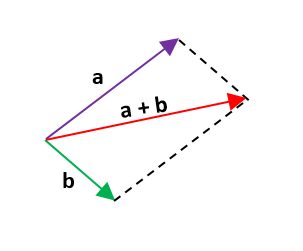
MÉTODO DEL PARALELOGRAMO

Sirve para sumar dos vectores con origen común. Se construye el paralelogramo trazando paralelas a los vectores dados. La resultante es la diagonal trazada desde el origen de los vectores.

Ejemplo: 

Donde |A|= 4u y |B|= 2u. Calcular: |A + B|

Actividad I.- Donde |A|= 3u y |B|= 5u. Calcular: |A+B|; sí forman un ángulo de 60° 

CASOS PARTICULARES

a.- Resultante máxima.- La resultante de dos vectores es máxima, cuando forman entre sí un ángulo de cero grados.

                                                                     R max = │A+B│

b.- Resultante Mínima.- La resultante de dos vectores es mínima cuando forman entre sí un ángulo de 180°.

                                                                        R min = │A - B│

c.- Resultante de dos vectores perpendiculares.- Cuando 2 vectores forman entre sí un ángulo recto, la resultante se obtiene aplicando el teorema de Pitágoras.

Ejemplo: Sí el módulo de la resultante máxima de 2 vectores es 28 y la mínima es 4. Calcular el módulo de la resultante de estos vectores cuando formen un ángulo de 90°.

DIFERENCIA DE DOS VECTORES

La diferencia de dos vectores que tienen el mismo origen se consigue uniendo los extremos de los vectores. El vector diferencia D indica el vector minuendo A.

                                      

El modulo del vector diferencia se determina aplicando:

Ejemplo.-

Sabiendo que: A=5 y B=8 ; forman un ángulo de 60°. Calcular ǀA-Bǀ

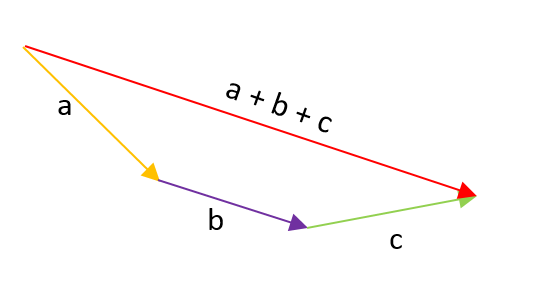
MÉTODO DEL POLÍGONO PARA SUMAR N VECTORES

Consiste en construir un polígono con los vectores sumados, manteniendo constante sus tres elementos(modulo, dirección y sentido), uniendo el extremo del primer vector con el origen del segundo vector, el extremo del segundo vector y el origen del tercer vector, así sucesivamente hasta el ultimo vector. El modulo del vector resultante se determina uniendo el origen del primer vector con el extremo del ultimo vector.

                                 

 

Ejemplo:

En el sistema vectorial mostrado, determinar el módulo del vector resultante.

Caso especial.- Si el polígono de vectores es ordenado (horario o antihorario) y cerrado, entonces la

 resultante es cero.

COMPONENTES RECTANGULARES DE UN VECTOR

Son aquellos vectores componentes de un vector que forman entre sí un ángulo de 90°.

VECTOR UNITARIO

Es un vector cuyo módulo es la unidad y tiene por misión indicar la dirección y sentido de un determinado vector. A dicho vector se le llama también versor.

VECTORES RECTANGULARES

Son aquellos vectores unitarios que se encuentran en los ejes coordenados rectangulares.

Ejemplo de aplicación:

En el sistema mostrado en la figura, expresar el vector "A" en términos de los vectores unitarios rectangulares, sabiendo que su módulo es de 30 unidades.

Solución:

SUMA DE VECTORES POR EL MÉTODO DE COMPONENTES RECTANGULARES

Para hallar la resultante por este método, se sigue los siguientes pasos:

1. Se descompone los vectores en sus componentes rectangulares.
2. Se halla la resultante en el eje x e y (Rx , Ry), por el método de vectores colineales.
3. El módulo del vector resultante se halla aplicando el teorema de Pitágoras.

Ejemplo:

En el sistema de vectores mostrado en la figura. Hallar el vector resultante y su módulo. 

Solución:

Actividad.- Dado un vector A de módulo 20 unidades, hallar sus componentes rectangulares (x ; y).